Optimizing Training Cost for Scalable Graph Processing

UC San Diego, Halıcıoğlu Data Science Institute

Authors: Han Hoang, Joshua Li
Mentors: Lindsey Kostas, Dhiman Sengupta

---

Introduction

Chip design often relies on place-and-route (PnR) tools, which iteratively arrange and connect millions of components (logic gates, wires, etc.) on a chip. While these traditional flows work, they can be time-consuming and labor-intensive, since each design iteration must carefully balance factors like performance, power consumption, and physical layout constraints.

A more efficient alternative is data-driven optimization, where machine learning models predict possible bottlenecks—such as congestion—early in the design cycle. With congestion insights in hand, designers can fine-tune component placement and wiring to reduce wasted resources, speeding up the entire process. A netlist helps in this task by modeling the circuit as a hypergraph: nodes represent components (like logic gates), and hyperedges capture their electrical connections.

DE-HNN (Demand-Estimating Hypergraph Neural Network) [1] is a leading approach for learning from this netlist structure. By using hierarchical virtual nodes to capture both local and long-range interactions in the graph, DE-HNN excels at predicting congestion or “demand.” However, it requires substantial compute power and memory, which can limit its practical use.

Our project focuses on optimizing DE-HNN’s training cost—reducing runtime or memory needs—while preserving, as much as possible, the model’s predictive accuracy on congestion. This balance between efficiency and performance is crucial for making advanced ML-based chip design viable in real-world production flows.

Methodology

Environment Setup

All experiments ran on UC San Diego’s DSMLP cloud system with an NVIDIA RTX A5000 GPU (24 GB VRAM), using PyTorch 2.2.2 and CUDA 12.2. This setup provided enough computational power and memory to handle large netlists and iterative optimization runs.

Dataset Description

We worked with six netlists that vary widely in size, ranging from about 460k to 920k nodes, with corresponding nets and edges. The first five netlists were used for training, while the sixth netlist served as our validation and test set.

Below is a summary of the main features used in our model:

Structural Features

• Node Degree: Number of edges connected to a node.
• Net Degree: Number of hyperedges connected to a net.
• Edge Connection: Indicates if there is an edge connecting a node to a net.
• Sink/Source Node: Specifies whether the node is a sink or source in its net.
• Number of Virtual Nodes: Total count of virtual nodes in the graph.

Spectral Features

• Top 10 Eigenvalues (Node): Largest eigenvalues of the node adjacency matrix.
• Top 10 Eigenvectors (Node): Corresponding eigenvectors for nodes.
• Top 10 Eigenvalues (Net): Largest eigenvalues of the net adjacency matrix.
• Top 10 Eigenvectors (Net): Corresponding eigenvectors for nets.

Representation Features

• Nodes Representations: Learned embeddings of individual nodes and their neighbors.
• Nets Representations: Learned embeddings of nets.
• Virtual Nodes Representations: Learned embeddings of the virtual (aggregate) nodes.

Target Variables

• Node Demand: Demand associated with each node.
• Net Demand: Demand associated with each net.

Training & Evaluation Strategy

Our model predicts demand (an indicator of congestion) by minimizing Mean Squared Error (MSE) on the training set. We monitor the validation loss to detect overfitting. Final results are reported on a dedicated test portion of netlist 6 to assess how well the model generalizes.

Optimization Strategy

We adopted an iterative optimization approach to make our DE-HNN model more resource-efficient while preserving accuracy. Each stage in this process addresses a different factor that could inflate training time or cause overfitting.

1. Early Stopping (ES)

   
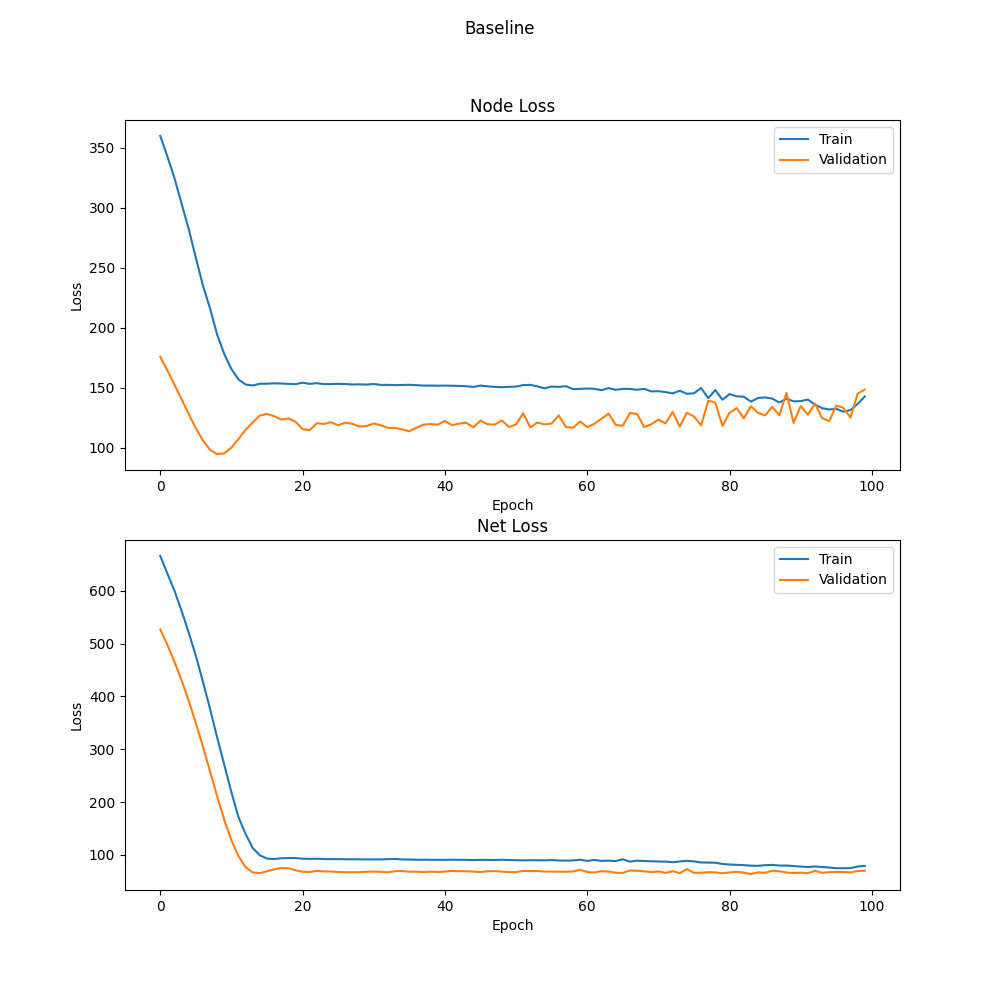
   Figure 1: Initial loss curves for the baseline model. The training loss keeps decreasing, while the validation loss stabilizes and eventually fluctuates, indicating potential overfitting.

   • Motivation: Prolonged training can cause overfitting, where the model becomes overly tuned to the training set and fails to generalize.
   • Method: We monitor the validation loss at each epoch and stop training early if it fails to improve beyond a specified tolerance for a certain number of epochs (patience).
   • Benefits: Saves computation time and prevents unnecessary training cycles once the model starts memorizing training data rather than learning generalizable patterns.

2. Architecture Adjustments (AA)

   • Motivation: DE-HNN can become large (many parameters) when using deep architectures or large embedding dimensions. This may consume excessive memory and increase runtime without guaranteeing better performance.
   • Method: We conduct a Grid Search on critical hyperparameters—such as the number of layers (e.g., 2–4) and the embedding dimensions (e.g., 8–32). We apply Early Stopping to each grid-search trial to further reduce training overhead.
   • Benefits: Identifies more efficient model configurations that still achieve solid accuracy but with reduced memory footprint and training time.
3. Dynamic Learning Rate (DLR)
   • Motivation: A fixed learning rate can cause slow convergence or getting stuck in local minima. Gradually decreasing the learning rate might help, but often requires trial-and-error to find the right schedule.
   • Method: We implement a Cyclical Learning Rate (CLR) [2], where the learning rate oscillates between a lower and upper bound within each cycle. This helps the model “jump out” of poor local minima and often converges faster.
   • Benefits: Eliminates manual tuning of step decay or exponential decay schedules, adapts dynamically to the training process, and can reduce total epochs needed.

Overall, each stage in this optimization pipeline—Early Stopping, Architecture Adjustments, and a Dynamic Learning Rate—targets a different facet of model complexity and convergence. By layering them together, we significantly cut down on training time and resource usage, while preserving DE-HNN’s strong performance in predicting IC congestion.

Baseline Model

Our baseline DE-HNN uses:

• 3 layers
• 32 dimensions (instead of the originally proposed 64, due to resource constraints)
• 100 training epochs

This baseline achieves:

• 133 MSE on Node loss
• 67.5 MSE on Net loss
• 5.05 minutes of total runtime
• ~22 GB of peak GPU memory usage

These results serve as a reference. Our optimizations aim to significantly reduce memory usage and runtime, ideally without sacrificing accuracy.

Results

Iterative Optimization

We tested three main optimization steps—Early Stopping, Architecture Adjustments, and a Dynamic Learning Rate (DLR)—to lower DE-HNN’s training time and memory usage while keeping its predictive performance as high as possible.

Early Stopping (ES)

Early Stopping halts training once validation loss stops improving within a specified tolerance, preventing unnecessary epochs where the model may overfit.

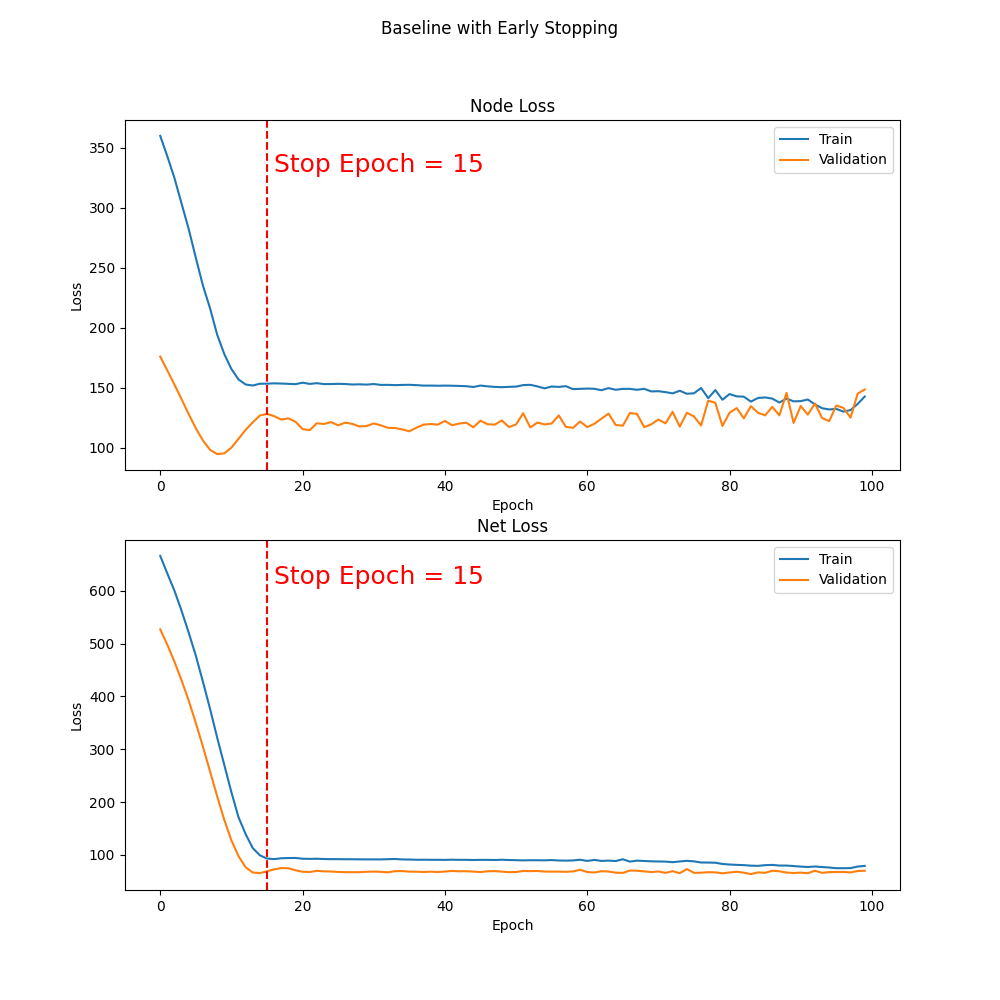
Figure 2: Early stoppage on baseline model.

• Key Findings
  • Training stopped at epoch 15 (instead of 100), cutting runtime by 84.37%.
  • Node MSE improved by 4.9%, Net MSE by 3.17%.
  • Peak memory usage stayed the same, but total training time dropped drastically.

In short, the baseline model was over-training well past epoch 15, and Early Stopping helped us achieve better validation performance in less time.

Architecture Adjustments (AA)

We systematically tested different DE-HNN configurations (2, 3, or 4 layers) paired with various embedding dimensions (8, 16, or 32). Early Stopping was applied to avoid training beyond the point of overfitting. Our goal was to find a balance between performance (Node/Net MSE) and resource savings (training time, memory usage).

Below are key heatmaps illustrating reduction in training cost and model performance in %:

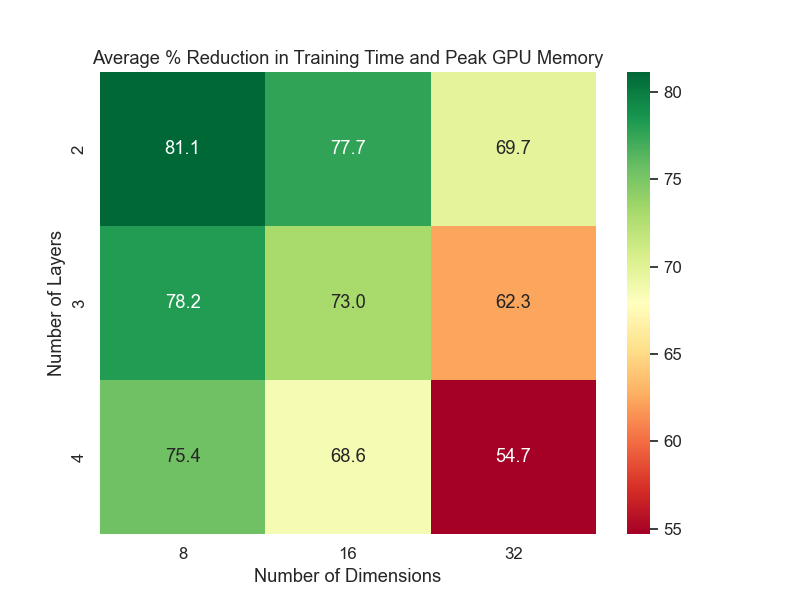
Figure 3: Average % reduction in training cost.

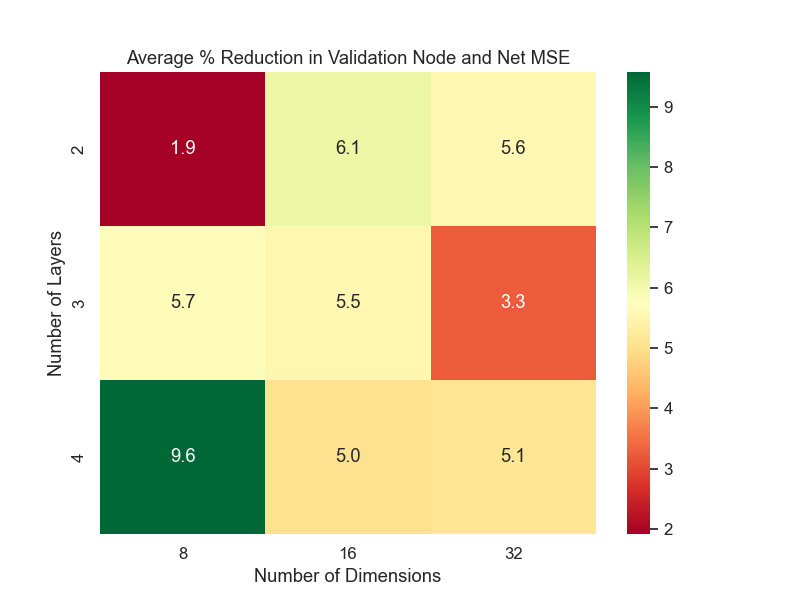
Figure 4: Average % reduction in model performance.

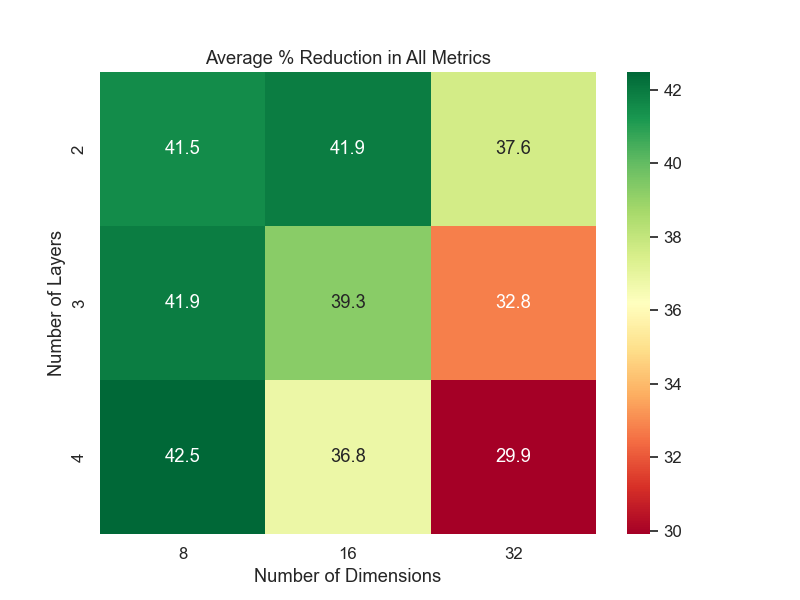
Figure 5: Average % reduction across computational cost and model performance.

We picked the model with 4 layers, 8 dimensions to be our Grid Search optimal model. The loss curves for this model is shown below:

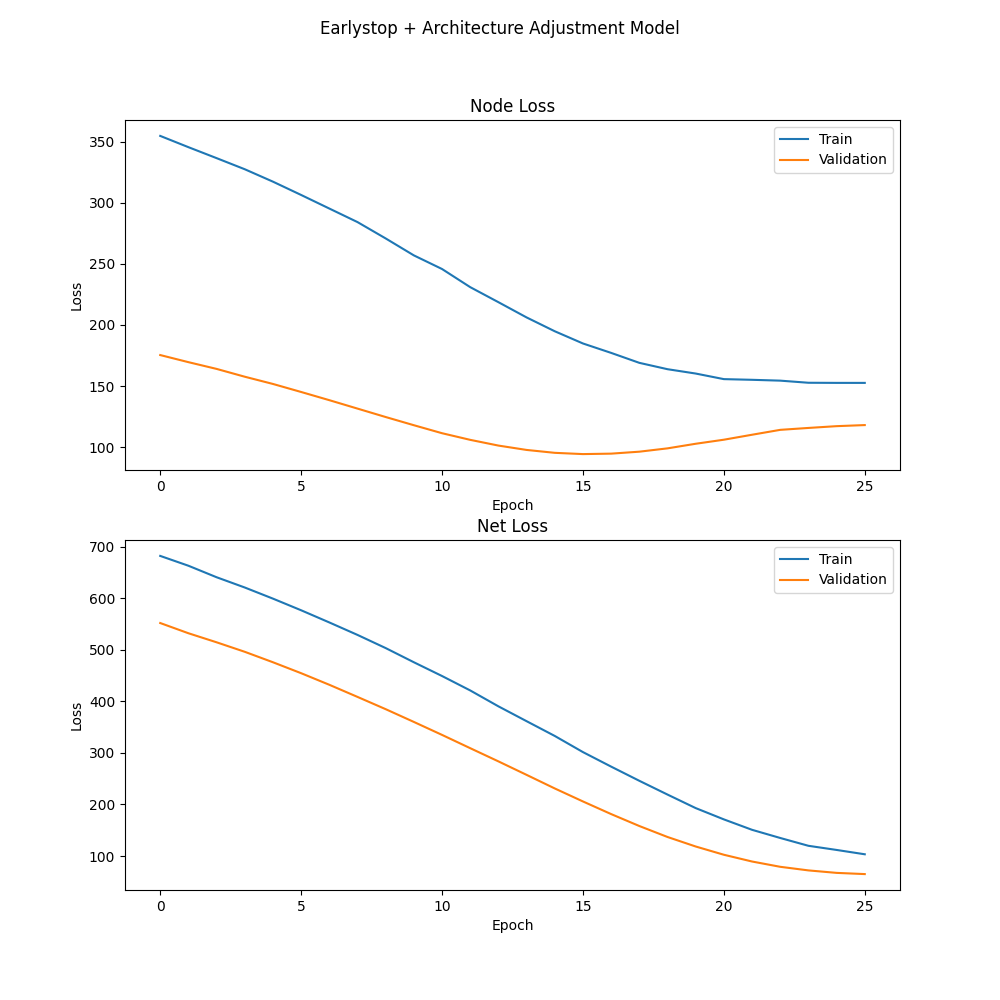
Figure 6: Validation loss remains stable, indicating less overfitting.

In summary:

• 4 layers / 8 dimensions generally offered the best trade-off.
• Some configurations (e.g., 2 layers, 8 dims) were more memory-efficient but had higher MSE.
• Embedding dimensions above 16 often increased memory/time without significantly better accuracy.

Dynamic Learning Rate (DLR)

Lastly, we introduced a Cyclical Learning Rate (CLR) that oscillates between minimum and maximum bounds in each cycle, helping the model skip local minima and converge faster.

Figure 7: CLR further reduces the required epochs, though Net MSE sees a trade-off.

• Key Outcomes:
  • Training often ended by epoch 11 (vs. 25 in Grid Search optimal model), a substantial cut from the 100-epoch baseline.
  • Node MSE reduced by 6.4%; Net MSE increased by 17.6%, showing that CLR helped one objective but introduced trade-offs in the other.
  • Memory savings from the previous steps persisted, and overall runtime was sharply reduced.

Despite the slight Net MSE compromise, DLR significantly shortened training, suggesting a valuable option for faster convergence when node-level demand accuracy is paramount.

Optimized Model

By stacking these optimizations, our final optimized model has achieved these statistics:

• Runtime dropped by 89.32%
• Memory usage decreased by 38.83%
• Node MSE decreased by 6.4%, and Net MSE increased by 17.6%, corresponding to a 6% average performance drop.

These results confirm that DE-HNN can be made significantly more practical by controlling overfitting (ES), reducing model complexity (AA), and speeding up convergence (DLR)—all while maintaining strong predictive accuracy for node demand.

Conclusion

Through a series of iterative optimizations, we transformed DE-HNN from a high-performing but computationally intensive model into a far more efficient and nearly equally accurate tool for predicting IC congestion:

• Simpler Architecture: A configuration of 4 layers and 8 dimensions significantly reduces memory footprint while still capturing the complexity of the netlist.
• Early Stopping: Stops training when validation loss stops improving, reducing epochs without compromising accuracy.
• Cyclical Learning Rate: Speeds up convergence by oscillating between a lower and higher learning rate, effectively shortening training time even further.

These results highlight the trade-off between performance and computational resources in real-world applications. By systematically combining Early Stopping, Architecture Adjustments, and a Dynamic Learning Rate, we’ve shown that DE-HNN can be scaled down to meet resource constraints while retaining most of its predictive power. This lays the groundwork for faster, more cost-effective congestion prediction in IC design.

References

[1] Luo, Zhishang, Truong Son Hy, Puoya Tabaghi, Donghyeon Koh, Michael Defferrard, Elahe Rezaei, Ryan Carey, Rhett Davis, Rajeev Jain, and Yusu Wang. (2024). DE-HNN: An effective neural model for Circuit Netlist representation. arXiv preprint, arXiv:2404.00477.

[2] Smith, Leslie N. 2015. “No More Pesky Learning Rate Guessing Games.” CoRR arXiv:1506.01186